低秩近似的方法：

  1. 伪逆矩阵：https://kexue.fm/archives/10366

  2. SVD分解：https://kexue.fm/archives/10407

  3. CR分解：https://kexue.fm/archives/10427

  4. 插值分解（ID）：https://kexue.fm/archives/10501

  5. CUR分解：https://kexue.fm/archives/10662

  6. Monarch矩阵：https://kexue.fm/archives/10249

Lora:

  1. 梯度视角下的Lora：https://kexue.fm/archives/9590
  2. 学习率对Lora的影响：https://kexue.fm/archives/10001
    • 核心结论：对于Lora AB，B的学习率 ηBη_B 要大于A的学习率 ηAη_A : ηB/ηA≈n/mn/rη_B/η_A ≈ n/m \sqrt{n/r}
  3. Lora改进1：https://kexue.fm/archives/10226
    • 核心结论：对于Lora AB不必有一个矩阵初始化为全零，可以初始化为 \begin{equation}W = (W_0 - A_0 B_0) + AB\end{equation}，即将原始W0W_0减去AB初始的初始值A0B0A_0 B_0，使用损失对 W0W_0 的初始梯度 G0G_0 进行SVD分解，G0=UΣVG_0=UΣV，取U的前r列初始化A，取V的第r+1∼2r行初始化B。初始值的第一步更新接近原始全量微调的更新
  4. Lora改进2：https://kexue.fm/archives/10266
    • 改进优化器或者说梯度计算方式，让AB的每一步更新尽可能接近全量微调的更新
  5. 有效秩：https://kexue.fm/archives/10847

SVD

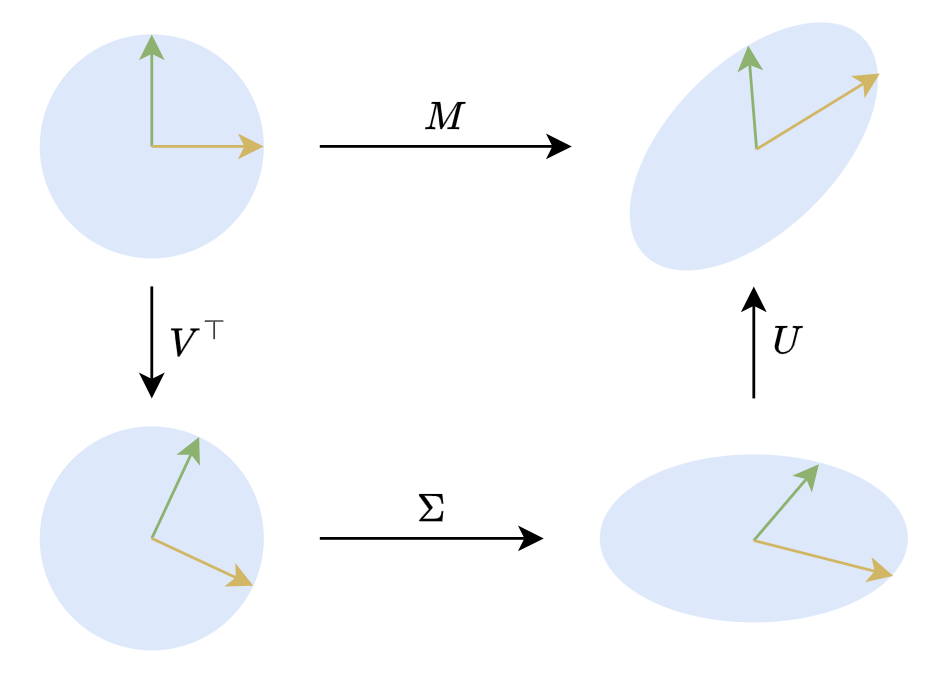
对于任意矩阵 M∈Rn×mM \in R^{n×m} ，都可以找到如下形式的奇异值分解（SVD，Singular Value Decomposition）：

M=UΣV⊤M=UΣV^⊤

其中 U∈Rn×n,V∈Rm×mU \in R^{n×n},V \in R^{m×m} 都是正交矩阵，Σ∈Rn×mΣ \in R^{n×m} 是非负对角矩阵：

Σi,j={σi,i=j0,i≠j\Sigma_{i,j} = \begin{cases} \sigma_i, & i = j \\ 0, & i \neq j \end{cases}

对角线元素默认从大到小排序，即 σ1≥σ2≥σ3≥⋯≥0σ_1≥σ_2≥σ_3≥⋯≥0 ，这些对角线元素就称为奇异值（Singular Value）。从数值计算角度看，我们可以只保留 ΣΣ 中非零元素，将 U,Σ,VU,Σ,V 的大小降低到 n×r,r×r,m×rn×r,r×r,m×r（ rr 是 MM 的秩），保留完整的正交矩阵则更便于理论分析。

在二维平面下，实矩阵的SVD有非常直观的几何意义。二维的正交矩阵主要就是旋转（还有反射，但几何直观的话可以不那么严谨），所以 Mx=UΣV⊤xMx=UΣV^⊤x 意味着任何对（列）向量x的线性变换，都可以分解为旋转、拉伸、旋转三个步骤，如下图所示：

img