毫米波雷达

毫米波雷达-AWR2243 —

简介

毫米波雷达，是工作在毫米波波段（Millimeter Wave ）探测的雷达。通常毫米波是指30～300GHz频域(波长为1～10mm)的。毫米波的波长介于微波和厘米波之间，因此毫米波雷达兼有微波雷达和光学雷达的一些优点。

同厘米波雷达相比，毫米波雷达具有体积小、质量轻和空间分辨率高的特点。与红外、激光、电视等光学雷达相比，毫米波雷达穿透雾、烟、灰尘的能力强，具有全天候(大雨天除外)全天时的特点。另外，毫米波雷达的抗干扰、反隐身能力也优于其他微波雷达。毫米波雷达能分辨识别很小的目标，而且能同时识别多个目标；具有成像能力，体积小、机动性和隐蔽性好，在战场上生存能力强。

目前在自动驾驶，智能监控领域广泛运用。毫米波雷达能直接获取目标的距离，速度，角度等基本信息。通过对数据的进一步处理，对目标的尺寸，轮廓可能也有一定的估计能力。

1 调频连续波(FMCW)

调频连续波(Frequency-Modulated Continuous Wave)，是一组幅值不变，但频率变化的连续波形，毫米波雷达使用的调频连续波是频率线性增加的正弦波，又叫线性调频连续波。

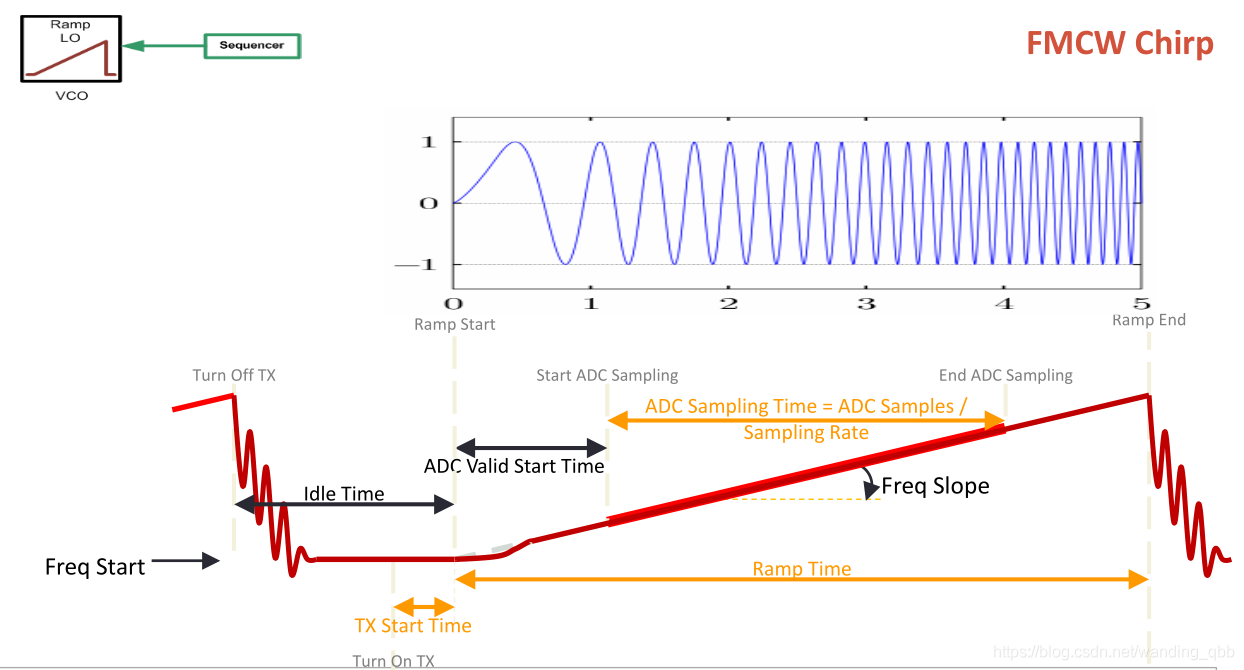
如下图的蓝色波形所示，横坐标是时间，横坐标是幅度，波的频率从起始频率逐渐增加到截至频率。这个过程称为一个Chirp(脉冲，啁啾)。

下方红色图，横坐标是时间，纵坐标是频率，更能直观的看出在每个Chirp中频率在线性增加，之后经过一个空闲时间迅速降到起始频率，开始下一个Chirp。

1.1、为什么毫米波雷达使用FMCW

由于线性调频波频率是随时间变化的，当毫米波发射出去，被远处的物体反射回来，可以很容易的根据回波的频率判断出波从发射到接收所经过的时间，从而根据电磁波的传播速度估算物体的距离。

很容易想到，能够测距离自然就能测速度，测量两次距离除以两次测量的时间就是速度。

进一步分析，可以发现角度也是可以通过距离计算出来的，通过多个雷达对同一目标的距离测量，可以根据细微的距离差，计算出目标的角度。

以上只是简单说明毫米波雷达测量距离，速度，角度的基本原理，下面将详细介绍雷达工作的各个细节，以及如何来设计FMCW，来满足自己对距离，速度，角度的分辨率要求，最大测量范围要求。

1.2、FMCW的基本参数

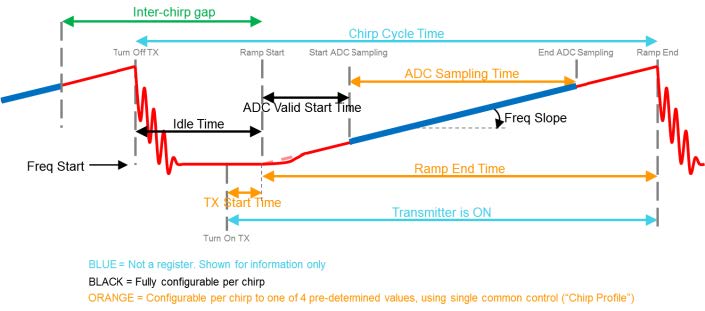
chirp：调频连续波信号。

startFreq：起始频率(GHz)。

idleTime：chirp与chirp之间的空闲时间(us)。

rampEndTime：调频时间(斜坡周期)，信号从起始频率上升到截止频率的时间(us)。

T_c ：chirp总周期，等于空闲时间+调频时间，即：T_c = idleTime + rampEndTime。

freqSlop(S)：调频连续波的频率变化斜率(MHz/us)。

ADCSamples(N)：数模转换采样数，后期数据处理需要使用的采样数据。

sampleRate(F_s)：数模转换采样速率(ks/s)。

ADCSamplingTime(T_s)：数模转换采样时间，等于采样数/采样速率，即 T_s = N/F_s, ADCSamplingTime = ADCSamples/sampleRate。

B：采样带宽，B = S * T_s = S * N/F_s = freqSlop * ADCSamples/sampleRate

periodicity(T_s)：帧时长，一个帧由多个chirp组成(ms)。

上面各参数的名称为代码中常使用的命名方式，括号内的简写便于后面推导公式使用。

1.2、距离

雷达的基本构造如下图所示：1. 频率合成器；2. 发射雷达；3. 接收雷达；4.混频器。

频率合成器用于生产线性调频波(FMCW)，之后通过发射雷达发射，雷达信号被目标反射后通过接收雷达接收信号，之后通过混频器生成发射信号和接收信号的差频信号(IF信号)。

差频信号(IF信号)的频率和距离正相关，如果距离为0，信号发射出去后立即反射接收，差频信号(IF信号)频率为0，距离越远，差频信号(IF信号)的频率越高。

推导距离与IF信号的关系表达式：

调频连续波斜率变化为 S，信号发射到接收的时间为 Δt，IF信号的频率为：f_IF = S * Δt，式中Δt即电磁波传播的时间，所有 Δt = 2 * d/c ，其中c是光速：3.0 * 10⁸。

$f_{IF} = S * 2 * d / c => d = \frac{f_{IF} *c }{2 * S}$

1.2.1 最大距离

最大距离取决于，IF信号的最大频率 f_{IF_max}，这取决于系统的硬件参数。一般毫米波雷达的的最大距离约200米左右。

1.2.2 距离分辨率

距离分辨率，同样取决于f_IF的分辨率。前面分析我们很容易计算出来距离与IF信号的关系。但真实情况下往往前方不止一个目标，接收到的回波信号是多种频率波的叠加。分析叠加信号的频率，可以通过傅里叶变换，把接收的时域信号在频域展开。对于离散的采样数据，通常使用快速傅里叶变换(FFT)。

傅里叶变换的频率分辨率与采样时间T_c成反比：Δf = 1/T_c，带入距离公式：

$$\Delta f_{IF} = S * 2 * \Delta d / c >= 1/T_c => \Delta d >= \frac{c}{2 * S *T_c}$$

式中S是斜波斜率，T_c是采样时间，所有S * T_C = B，是采样带宽。

综上，距离分辨率：

$$\Delta d = \frac{c}{2 * B}$$

可以知道，距离分辨率与带宽成反比，带宽越高，距离分辨率越小。

1.3、速度

根据多普勒效应，机械波满足如下公式，其中：f^′是接收到的频率；f是发射源于该介质中的原始频率；v 是波在该介质的传播速度；v₀是接收者的移动速度； v_s是发射源的移动速度；

$f' = (\frac{v +- v_0}{v-+v_s})f$

但对于电磁波，多普勒效应更加复杂，且物体的运动速度一般相对光速几乎可忽略不计，因此不易通过频率频率获取目标速度。

速度的估算，正如基本原理所介绍的那样，是通过测量距离的变化估算的。

距离的变化，可以通过相位判断。对速度估算，需要发射一组N个等间隔的线性调频脉冲(chirp)，称为帧(Frame)，通过分析一帧内每个chirp的相位变化，估算速度。

距离变化与相位变化的关系：最简单的假设，一个初始相位为0的毫米波波射向距离为0的物体，回波的相位也是0，射向距离1/8波长的物体，回波的相位是 2 * 1/8 * 2π；同理一个波在某一时刻 t0 射向距离为 d 的物体，下个时刻 t0 + T_c 射向 d + Δd 的物体，遵循同样的规律，$Δω = 2* Δd/$，这里虽然是线性调频波，波长在变化，但是由于波长的变化量相对起始波长相差至少一个数量级，所有可以忽略不记，可以任务相位变化是和频率无关的。

又因为 Δd = v * T_c，所以可得速度估算公式：

$$Δω = \frac{2 * v* T_c }{\lambda} * 2\pi = \frac{4\pi * v * T_c}{\lambda} => v = \frac{Δω * \lambda}{4\pi * T_c}$$

1.3.1 最大速度

最大速度取决于最大相位角，为了不造成歧义，约定 |Δω| < π，大于0是远离，小于0是接近。

所以有：$|Δ\omega| = |\frac{4\pi * v * T_c}{\lambda}| < \pi => v< \frac{λ}{4T_c}$

即物体运动的最大速度不能超过$\frac{λ}{4T_c}$，式中λ 是波长，T_c是是chirp总周期。(如果T_c容易搞混，可以考虑物体在 chirp的空闲时间或者不采样时也是运动的，所以是除chirp总周期，不是斜坡时间，也不是采样时间)

1.3.2 速度分辨率

速度分辨率同样取决于相位角频率 Δω的分辨率，因为接收的信号是多个物体的速度叠加，因此不能通过简单相位法得到速度。同样是通过快速傅里叶变换，将回波信号在频域展开，获取频率。

快速傅里叶变换的分辨率：对于离散的相位角频率满足 Δω > = 2 * π/M(radians/samples)，或者Δω > = 1/M(cycles/sample) 这里M是采样点数，即每帧的chirp数。

可以看出离散数据的分辨率，和连续数据的分辨率形式上是非常相似的(Δf = 1/T_c)。离散数据和采样点数相关，连续数据和采样时间相关。

速度分辨率推导过程：

$= 2/ M => = 2/ M => v = = $

1.4、角度

角度的测量需要多个接收雷达，根据不同接收雷达接收信号的的微小距离差来评估角度。如下图所示，假设物体足够远(一般来说相对雷达的间距是足够远的)。发射雷达TX发射信号，接收雷达RX接收回波信号。RX1与RX2接收的信号是近似平行的。因此两者的信号传播距离差可以表示为：

Δd = dsin(θ)，这里d表示两个RX的距离。

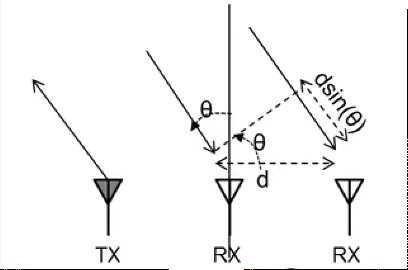
由上一节速度评估的分析可知，距离差和相位之间相关。

这里距离与相位的关系为：

$\Delta \phi = \frac{2\pi \Delta d} {\lambda}$

可以看到测角与测速的相位变化：$\Delta \phi = \frac{4\pi \Delta d} {\lambda}$，存在二倍关系，是因为测角时电磁波去的时候距离相同，只有来的时候有距离差。（ps：下图滥用了符合，d表示物体与雷达的距离，而不是上图两个接收雷达的间距）

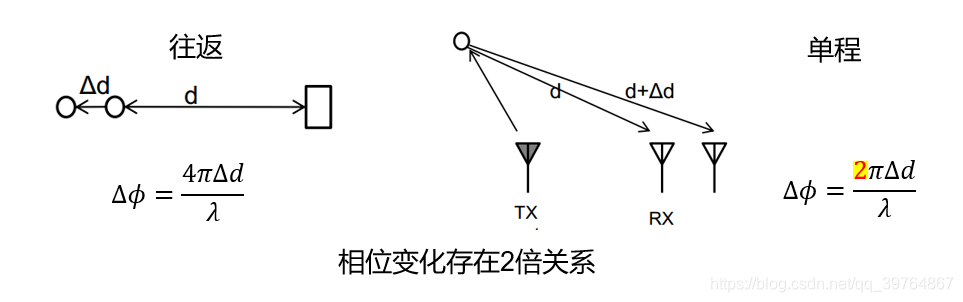
带入可得：

$\Delta \phi = \frac{2\pi \Delta d} {\lambda} = \frac{2\pi dsin(\theta)} {\lambda}$

即：$\theta = arcsin(\frac{\lambda*\Delta \phi}{2\pi d})$

1.4.1最大角度

与最大速度类似，最大角度取决于两个雷达之间的最大相位角，为了不造成歧义，约定 |Δϕ| < π。可得：

$|\Delta \phi| = \frac{2\pi dsin(\theta)} {\lambda} < \pi => |\theta| < arcsin(\frac{\lambda}{2d})$

一般毫米波雷达的间距 d = λ/2，所以 |θ| < π/2。

雷达的最大可视角度为正负 90度。

1.4.2 角度分辨率

角度分辨率也和速度分辨率类似，由于可能存在多个物体导致回波叠加，因此同样需要使用快速傅里叶变换对回波信号进行处理。而这里也是离散信号，采样点是接收雷达RX的个数。在速度估算时，我们说过离散信号的分辨率取决与采样点的个数，所以这里相位分辨率为：

Δϕ > 2π/N，式中N是接收雷达的个数。

所以：

$= {} > 2/N => > arcsin() => > arcsin() $

上式Nd，就是雷达阵列的宽度，可见当波长一定时，雷达的角分辨率与雷达阵列尺寸有关，分辨率越大，需要的雷达阵列的尺寸就越大。由于一般 d = λ/2 ，所以角度和接收雷达的个数相关。

2 德州仪器(TI) 产品使用

2.1 MIMO雷达

2.2 AWR 2243

2.3 DCA 1000

2.4 mmWave Studio

3 雷达数据的处理

3.1、格式处理

TI公司的毫米波雷达通常使用DCA 1000 或 TSW 1400进行数据采集，这里主要分析DCA 1000采集的数据格式。

3.1.1 使用DCA 1000采集的xWR12xx或xWR14xx实数数据格式

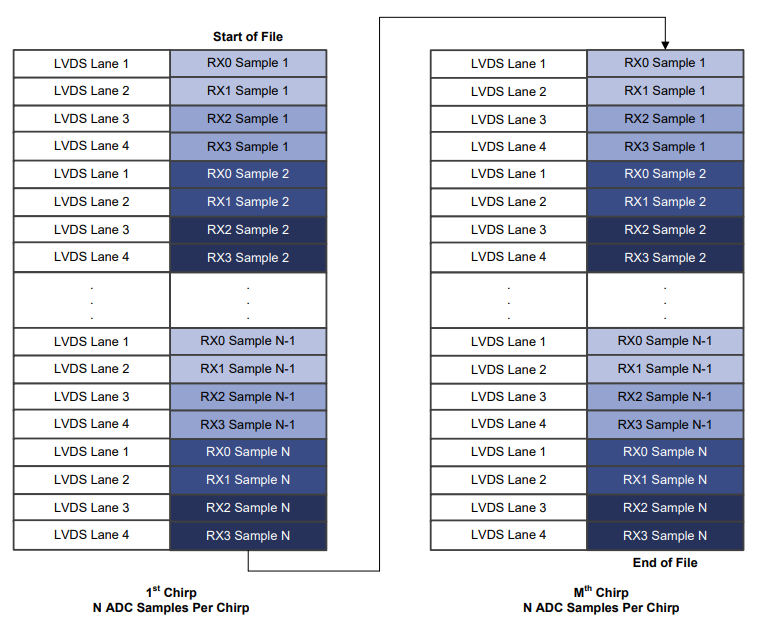
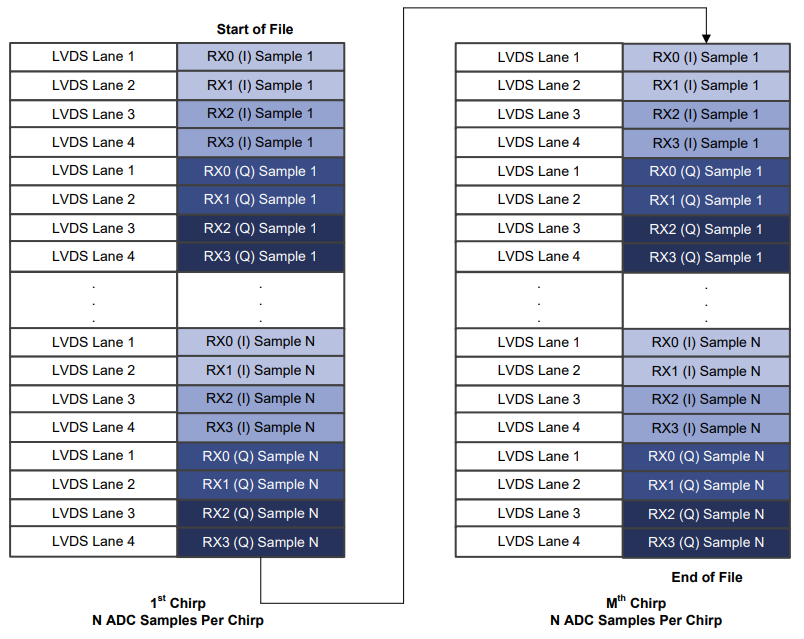
3.1.2 使用DCA 1000采集的xWR12xx或xWR14xx复数数据格式

matlab行优先

python列优先

返回：(numLoopsPerFrame * numTxAntennas, numRxAntennas, numRangeBins)

def organize2243(raw_frame, num_chirps, num_rx, num_samples):
    """Reorganizes raw ADC data into a full frame

        Args:
            raw_frame (ndarray): Data to format
            num_chirps: Number of chirps included in the frame
            num_rx: Number of receivers used in the frame
            num_samples: Number of ADC samples included in each chirp

        Returns:
            ndarray: Reformatted frame of raw data of shape (num_chirps, num_rx, num_samples)

        """
    ret = np.zeros(len(raw_frame) // 2, dtype=complex)

    # Separate IQ data 
    # [n_chirp, n_Rx, n_simples/2, 2, 2]->[n_chirps, n_RX, n_simples]
    # AWR1243 [n_chirp, n_simples, 2, n_Rx] -> [n_chirps, n_simples, n_RX]
    ret[0::4] = raw_frame[0::8] + 1j * raw_frame[4::8]
    ret[1::4] = raw_frame[1::8] + 1j * raw_frame[5::8]
    ret[2::4] = raw_frame[2::8] + 1j * raw_frame[6::8]
    ret[3::4] = raw_frame[3::8] + 1j * raw_frame[7::8]
    # 交换维度 [n_chirps, n_simples, n_RX] -> [n_chirps, n_RX, n_simples]
    ret = ret.reshape((num_chirps, num_samples, num_rx))
    ret = np.swapaxes(ret, 1, 2)

    return ret.reshape((num_chirps, num_rx, num_samples))

3.1.3 使用DCA 1000采集的xWR16xx或IWR6843实数数据格式

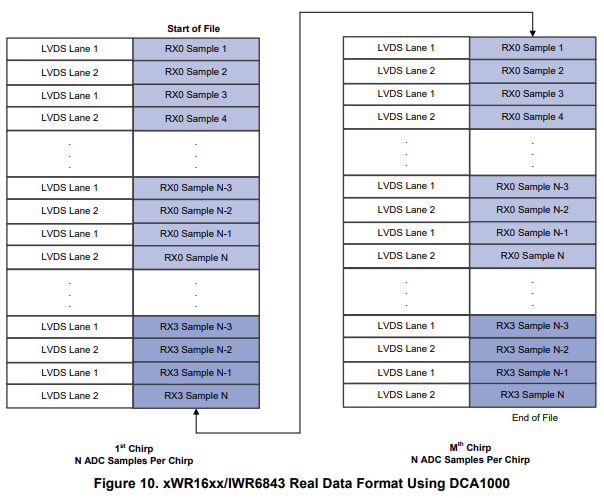
3.1.3 使用DCA 1000采集的xWR16xx或IWR6843复数数据格式

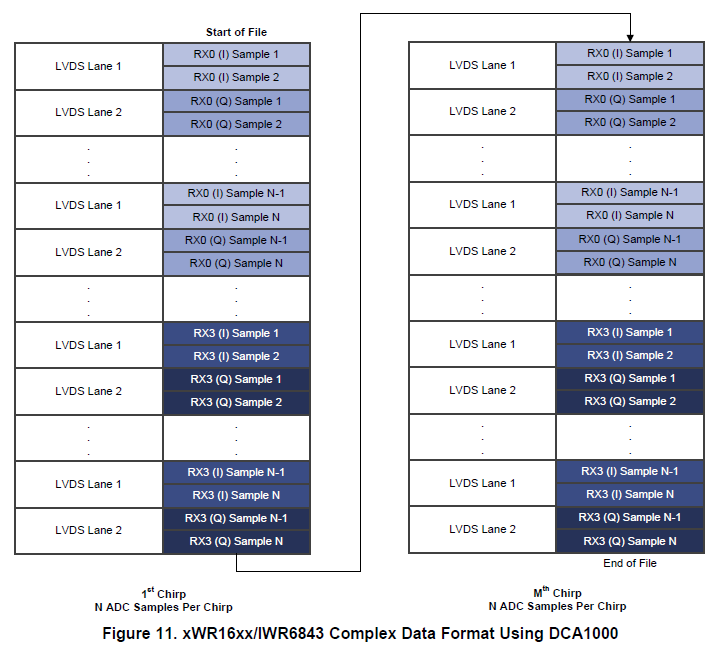
返回：(numLoopsPerFrame * numTxAntennas, numRxAntennas, numRangeBins)

def organize(raw_frame, num_chirps, num_rx, num_samples):
    """Reorganizes raw ADC data into a full frame

        Args:
            raw_frame (ndarray): Data to format
            num_chirps: Number of chirps included in the frame
            num_rx: Number of receivers used in the frame
            num_samples: Number of ADC samples included in each chirp

        Returns:
            ndarray: Reformatted frame of raw data of shape (num_chirps, num_rx, num_samples)

        """
    ret = np.zeros(len(raw_frame) // 2, dtype=complex)

    # Separate IQ data 
    # [n_chirp, n_Rx, n_simples/2, 2, 2]->[n_chirps, n_RX, n_simples]
    ret[0::2] = raw_frame[0::4] + 1j * raw_frame[2::4]
    ret[1::2] = raw_frame[1::4] + 1j * raw_frame[3::4]

    return ret.reshape((num_chirps, num_rx, num_samples))

分离TX数据

(numLoopsPerFrame * numTxAntennas, numRxAntennas, numRangeBins) -> (numLoopsPerFrame, numTxAntennas * numRxAntennas, numRangeBins)

def separate_tx(signal, num_tx, vx_axis=1, axis=0):
    """Separate interleaved radar data from separate TX along a certain axis to account for TDM radars.
    从单独的TX沿某一轴将交错的雷达数据分离，以描述TDM雷达。
    Args:
        signal (ndarray): Received signal.
        (numChirpsPerFrame, numRxAntennas, numRangeBins)
        num_tx (int): Number of transmit antennas.
        vx_axis (int): Axis in which to accumulate the separated data.
        用于累积分离数据的轴。
        axis (int): Axis in which the data is interleaved.
        数据交错的轴。

    Returns:
        ndarray: Separated received data in the

    """
    # Reorder the axes
    # 维度交换，将待处理的维度交换到第0维
    reordering = np.arange(len(signal.shape))
    reordering[0] = axis
    reordering[axis] = 0
    signal = signal.transpose(reordering)

    # 因为发TX雷达是分时的，numChirpsPerFrame = numLoopsPerFrame * numTxAntennas
    # 这里是先取出同一个TX雷达数据(numLoopsPerFrame, numRxAntennas, numRangeBins)，
    # 将取出的数据，沿原本的RX轴，即vx_axis = 1的轴拼接 (numLoopsPerFrame, numTxAntennas * numRxAntennas, numRangeBins)
    # 相当于 (numLoopsPerFrame * numTxAntennas, numRxAntennas, numRangeBins) ->
    # (numLoopsPerFrame, numTxAntennas * numRxAntennas, numRangeBins)
    # 感觉这里可以直接reshape，效果应该一样，因为展成一维，数据位置并没有变动
    out = np.concatenate([signal[i::num_tx, ...] for i in range(num_tx)], axis=vx_axis)

    return out.transpose(reordering)

3.2、距离

## 加窗
fft1d_in = np.hamming(frame.shape[-1])
rangeBins = np.fft.fft(fft1d_in, axis=2)

3.3、速度

fft2d_in = np.transpose(rangeBins, axes=(2, 1, 0))
fft2d_in = np.hamming(fft2d_in.shape[-1])
fft2d_out = np.fft.fft(fft2d_in, axis=-1)
fft2d_out = np.fft.fftshift(fft2d_out, axes=-1)
range_doppler = np.transpose(fft2d_out, axes=(2, 1, 0))
range_doppler = range_doppler[:, 0, :]

3.4、角度

dopplerBins = aoa_input
padding = ((0, 0), (0, numAngleBins-dopplerBins.shape[1]), (0, 0))
# (numRangeBins, numAzimuthBins， numDopplerBins)
range_azimuth = np.pad(dopplerBins, padding, mode='constant')
"""
数组填充：
填充的数组：dopplerBins
填充的形状：padding
填充模式：constant 常量填充，默认0
"""
print(range_azimuth.shape)
# print(range_azimuth)  # (Range, azimuth, Doppler)
range_azimuth = np.fft.fft(range_azimuth, axis=1)

4 信号处理相关算法

4.1 杂波去除

4.2 目标检测

4.3 目标追踪

参考连接：

https://www.zhihu.com/question/455439504/answer/1901513398

相机数据是结构化的高分辨率图像数据，毫米波雷达原始数据则是角分辨率很低且没有高程信息的稀疏点云，这二者原始数据很难融合成一套输入给到神经网络模型，因此目前绝大多数方案都是使用后融合（松耦合）方案。

https://zhuanlan.zhihu.com/p/92887546